Today I am going to discuss Volume of 14 Geometrical Shapes for Billing in Civil Engineering with examples which we use in daily life on Construction Site.
Contents
- 1 VOLUME OF 14 DIFFERENT GEOMETRICAL SHAPES
- 1.1 CUBE
- 1.2 RECTANGULAR PRISM
- 1.3 TRIANGULAR PRISM
- 1.4 RIGHT ANGLE TRIANGULAR PRISM
- 1.5 RIGHT CIRCULAR CYLINDER
- 1.6 VOLUME OF SPHERE
- 1.7 RIGHT CIRCULAR CONE
- 1.8 VOLUME OF FRUSTUM
- 1.9 VOLUME OF PARABOLIC CONE
- 1.10 VOLUME OF ELLIPTICAL CONE
- 1.11 VOLUME OF SQUARE PYRAMID
- 1.12 VOLUME OF TRAPEZOID PYRAMID
- 1.13 VOLUME OF POLYGON PRISM
- 1.14 VOLUME OF POLYGON PYRAMID
- 2 REFERENCE VIDEO
VOLUME OF 14 DIFFERENT GEOMETRICAL SHAPES
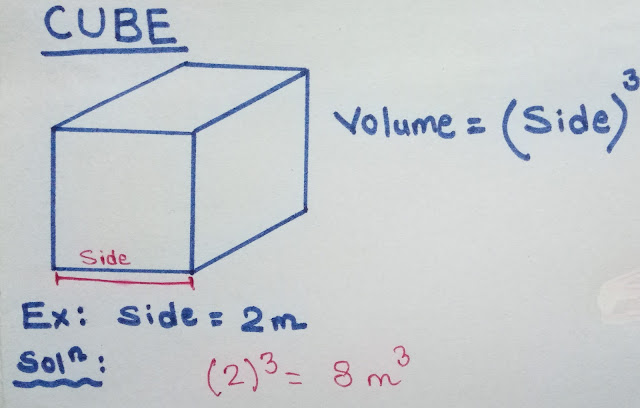
CUBE
In civil engineering, calculating the volume of a cube is often used for billing purposes, especially when estimating the amount of material needed for construction or other projects.
When calculating the volume for billing in civil engineering, this value is crucial for accurately estimating the amount of concrete, soil, or any other material that will be required for a specific project. It helps in planning and budgeting for the necessary resources, ensuring that the right quantities are ordered and used, minimizing waste and cost overruns.
The volume of a cube can be determined by using the formula:
VOLUME = Side x Side x Side
RECTANGULAR PRISM
In civil engineering, determining the volume of a rectangular prism is vital for billing purposes, especially when estimating the necessary materials for construction projects.
The volume of a rectangular prism can be calculated using the formula:
VOLUME = Length x Breadth x Height

TRIANGULAR PRISM
A triangular prism is a three-dimensional geometric shape with two triangular bases and three rectangular or parallelogram faces connecting the corresponding sides of the triangles. The triangular bases can be of different sizes or identical, and the connecting faces are always rectangles or parallelograms.
Triangular prisms are commonly encountered in various fields, including architecture and civil engineering, where they might represent elements of structures like roofs, beams, or supports. They’re also useful in geometry as a way to understand the relationship between different 2D and 3D shapes.
VOLUME = (Base x Height x Width) / 2

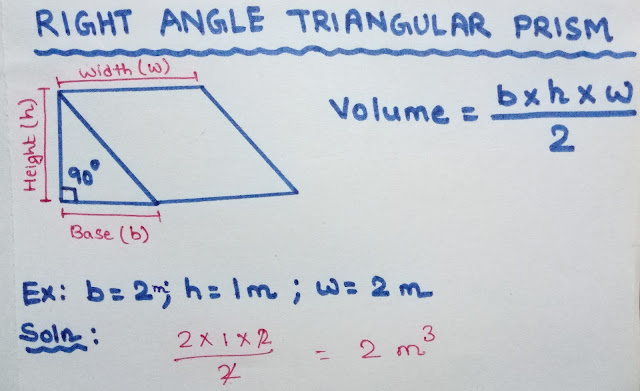
RIGHT ANGLE TRIANGULAR PRISM
VOLUME = (Base x Height x Width) / 2
RIGHT CIRCULAR CYLINDER
A right circular cylinder is a three-dimensional geometric shape that consists of two parallel circular bases connected by a curved surface, forming a cylinder with straight sides. The term “right” indicates that the axis of the cylinder is perpendicular to the center of the circular bases.
Formula = π x Radius x Radius x Height

VOLUME OF SPHERE
A sphere is a three-dimensional geometric shape that is perfectly round and symmetrical in all directions. It is defined as the set of all points in three-dimensional space that are equidistant from a single central point. The distance from the center of the sphere to any point on its surface is called the radius.
Formula = (4 x π x Radius x Radius x Radius) / 3

RIGHT CIRCULAR CONE
A right circular cone is a three-dimensional geometric shape that features a circular base and a curved surface that tapers up to a single point called the apex. The term “right” indicates that the apex is directly above the center of the base, and the axis connecting the apex and the center of the base is perpendicular to the base.
Formula = (π x Radius x Radius x Height) / 3

VOLUME OF FRUSTUM
A frustum is a three-dimensional geometric shape that resembles a cone but with its top portion sliced off by a plane parallel to the base. As a result, a frustum has two parallel circular bases of different sizes, connected by a curved surface. It’s also referred to as a “truncated cone.”

VOLUME OF PARABOLIC CONE
A parabolic cone, also known as a conical paraboloid, is a three-dimensional geometric shape that resembles a cone but is formed by a parabolic curve rotated around its axis. This shape is defined by a quadratic equation in two variables that generates a parabolic cross-section.
Formula = (2 x π x Diameter x Diameter x Height) / 15

VOLUME OF ELLIPTICAL CONE
An elliptical cone is a three-dimensional geometric shape that is formed by rotating an ellipse around one of its axes. It shares similarities with both a cone and an ellipse but has its own distinct characteristics.
Formula = (π x Diameter x Diameter x Height) / 6

VOLUME OF SQUARE PYRAMID
A square pyramid is a three-dimensional geometric shape with a square base and four triangular faces that meet at a single point called the apex. It is one of the simplest types of pyramids and is characterized by its symmetrical structure.
Formula = (Side x Side x Height) / 3

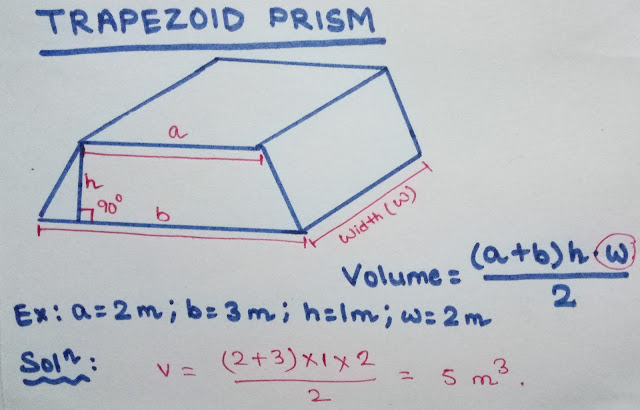
VOLUME OF TRAPEZOID PYRAMID
A trapezoid pyramid, also known as a trapezoidal pyramid, is a three-dimensional geometric shape with a trapezoidal base and four triangular faces that converge at a single point called the apex. It’s a variation of a pyramid where the base is not a regular polygon like a square.
VOLUME OF POLYGON PRISM
A polygonal prism, also known as a polyhedral prism, is a three-dimensional geometric shape formed by connecting two congruent polygonal bases with rectangular or parallelogram faces. The bases are connected by a series of rectangular or parallelogram sides, creating a prism-like structure with multiple sides.
Formula = Area of Base x Height
Where, Area = (Apothem x Perimeter) / 2

VOLUME OF POLYGON PYRAMID
A polygonal pyramid, also known as a polyhedral pyramid, is a three-dimensional geometric shape that has a polygonal base and triangular faces that meet at a single point called the apex. It is formed by extending the sides of the polygonal base to the apex and creating triangular faces along the way.

REFERENCE VIDEO
If you want detailed knowledge, then watch this Reference video on YouTube Channel: Learning Civil Technology. Because many important points have been covered during the making of the video, so Must Watch. The link is given below:
SOURCE: LEARNING CIVIL TECHNOLOGY
You can also follow me on Instagram, Telegram, and Facebook page. Because of many small things, which are very important from an interview point of view, it is not possible to put them here, I put all that on Instagram, Telegram, and Facebook page. You can take it from there. You will find the links to all social media below.
INSTAGRAM | TELEGRAM | FACEBOOK PAGE
SHARE THIS POST, IF YOU LIKE IT !! THANKS






