Today I am going to discuss Area of 10 Geometrical Shapes for Billing in Civil Engineering with examples which we use in daily life on Construction Site
Contents
AREA OF DIFFERENT GEOMETRICAL SHAPES
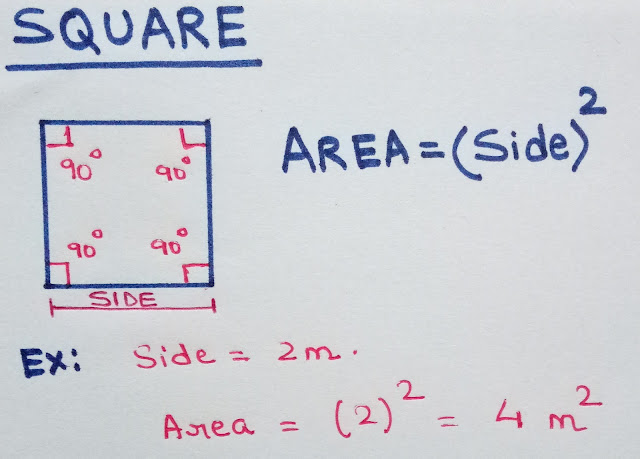
SQUARE
A square is a two-dimensional geometric shape that has four sides of equal length and four right angles (90-degree angles). It is a regular quadrilateral, meaning all its sides and angles are congruent (equal). The opposite sides of a square are parallel, and the diagonals bisect each other at a 90-degree angle.
AREA = (Side x Side) unit square
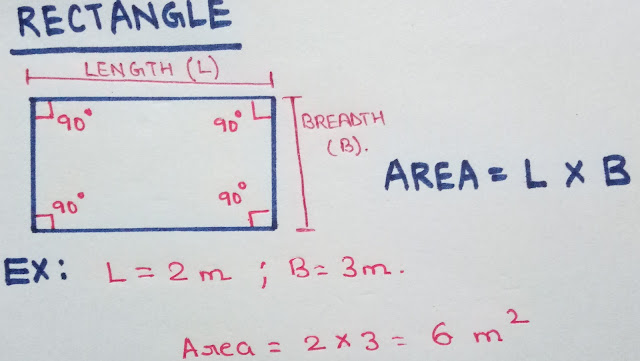
RECTANGLE
A rectangle is a two-dimensional geometric shape with four sides and four right angles (90-degree angles). Unlike a square, a rectangle’s opposite sides are of different lengths, but the angles remain right angles. It is also a regular quadrilateral, meaning it has equal opposite angles and congruent opposite sides.
AREA = (Length X Breadth) unit square
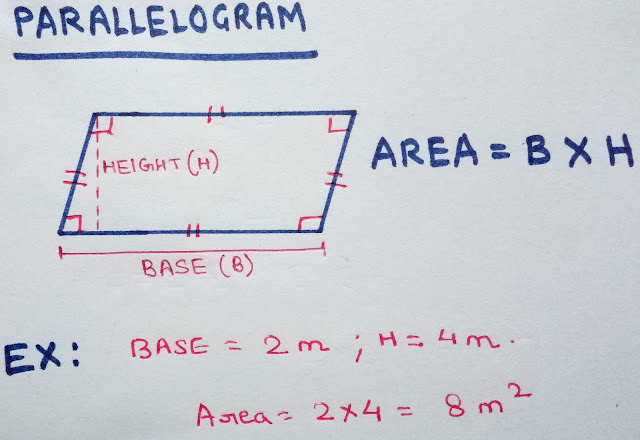
PARALLELOGRAM
A parallelogram is a two-dimensional geometric shape with opposite sides that are parallel to each other. It has four sides and four angles. The opposite sides of a parallelogram are equal in length, and the opposite angles are congruent (equal).
AREA = (Base X Height) unit square
- Also Read: Quantity Of Tiles For Wall & Cladding
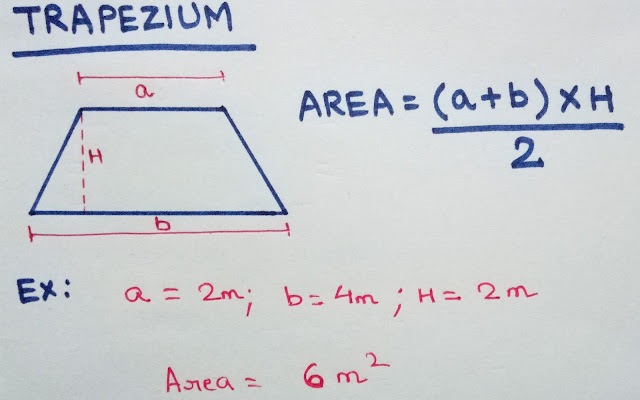
TRAPEZIUM
A trapezium, known as a trapezoid in American English, is a two-dimensional geometric shape with four sides. It is characterized by having one pair of opposite sides that are parallel, while the other pair of opposite sides are not parallel. The term “trapezium” is more commonly used outside of North America, while “trapezoid” is used in North America.
AREA = ((Sum of Parallel sides) X Height ) / 2
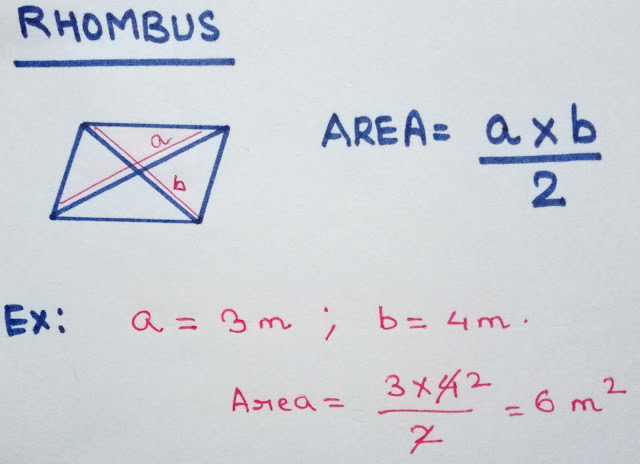
RHOMBUS
A rhombus is a two-dimensional geometric shape with four sides of equal length. It is a type of parallelogram where all sides are congruent (equal), and opposite sides are parallel to each other. Additionally, a rhombus has the unique property that all its angles are equal.
AREA = (Product of Diagonals) / 2
REGULAR POLYGON
A regular polygon is a two-dimensional geometric shape that has all its sides of equal length and all its angles of equal measure. In essence, it is a polygon where all the sides and angles are congruent (equal). Regular polygons are characterized by their symmetry and uniformity.
AREA = (Radius of Inscribed Circle X Perimeter of Polygon) / 2

CIRCLE
A circle is a two-dimensional geometric shape defined as the set of all points in a plane that are equidistant from a central point called the center. It is one of the most fundamental shapes in geometry, characterized by its curved boundary.
AREA = π x (Radius x Radius)

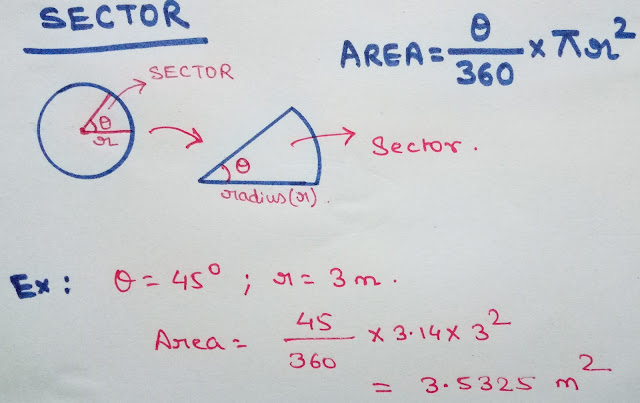
SECTOR
A sector is a portion of a circle that is defined by two radii and the arc between them. It is a two-dimensional region that is shaped like a slice of pie or a wedge. Sectors are used to measure and represent parts of a circle, particularly in terms of angles and areas.
AREA = (θ x π x (Radius x Radius) ) / 360
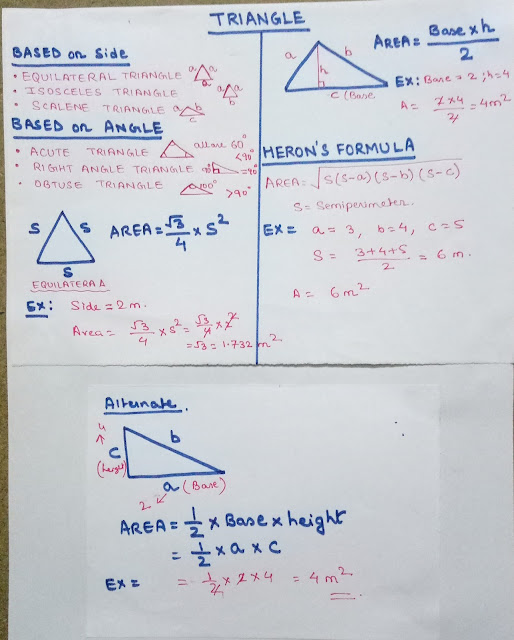
TRIANGLE
A triangle is a two-dimensional geometric shape with three sides and three angles. It is one of the simplest and most fundamental shapes in geometry, serving as a building block for more complex polygons and shapes.
ELLIPSE
An ellipse is a two-dimensional geometric shape that resembles a stretched or squished circle. It is defined as the set of all points in a plane for which the sum of the distances from two fixed points (called the foci) is constant. An ellipse has a unique property: the sum of the distances from any point on the ellipse’s boundary to the two foci is always the same.
AREA = π x Major Axis Radius x Minor Axis Radius

REFERENCE VIDEO
If you want detailed knowledge, then watch this Reference video on YouTube Channel: Learning Civil Technology. Because many important points have been covered during the making of the video, so Must Watch. The link is given below:
SOURCE: LEARNING CIVIL TECHNOLOGY
You can also follow me on Instagram, Telegram, and Facebook page. Because of many small things, which are very important from an interview point of view, it is not possible to put them here, I put all that on Instagram, Telegram, and Facebook page. You can take it from there. You will find the links to all social media below.
INSTAGRAM | TELEGRAM | FACEBOOK PAGE
SHARE THIS POST, IF YOU LIKE IT !! THANKS