Hello friends. This is Mukesh from Learning Technology. Aaj ke video me mai apko bataunga How to Calculate Cutting Length of Trapezium Shape Stirrups at Construction Site in details.

Mujhe pata hai ap log sab iske liye bahut excited ho. To chaliye copy pen le ke baith jaiye aur ha ek request hai apse, agar ye post apko pasand aye to ise jarur apne Civil Engineer friends aur juniors ke sath jarur share jarur kare. Kiu ki kuch responsibility apki bhi hain is Nation ko aage badhane mein.

To chaliye post ki taraf aage badhte hain.

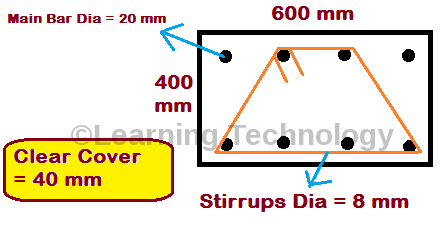
Sab se pehle upar diye hue Figure me given kya kya hain use check kar lete hain.

Column ka size hain = 600 mm x 400 mm

Main Vertical Bar ka diameter maine yaha consider kiya hain = 20 mm

Clear Cover = 40 mm (Concrete Surface aur Stirrups ke Outer Face ke bich ke gap ko Clear Cover kehte hain)

Trapezium Shape Stirrups, Jiska hame Cutting Length nikalna hai uska diameter maine consider kiya hain = 8 mm

Trapezium Shape ka Cutting Length nikalne ke lie hame ek chij pehle se nikal ke rakh lena hoga. Wo hain Centre to Centre Distance of Main Vertical Bar.

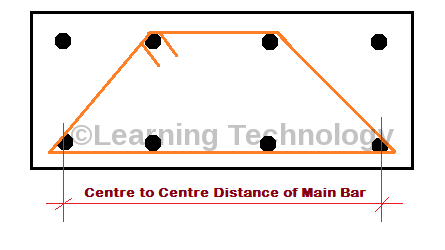
{(Length of Column) – (2 x Clear Cover) – (2 x Stirrups Dia) – (2 x Half of Main Vertical Bar Dia)} / (Number of Equal Division in between Main Vertical Bar)

= {600 – (2 x 40) – (2 x 8) – (2 x 10)} / 3

= (600 – 80 – 16 – 20) / 3

= 484 / 3

= 161 mm

Ab ap niche diye hue Figure me dekhenge ki maine Trapezium Shape Stirrup ka Single Line Diagram banaya hain aur maine har side ko ek name diya hain. Jaise BASE length ko maine consider kia hain ‘A’, TOP length ko maine consider kiya hain ‘B’ aur SIDE ke dono length ko maine consider kiya hain ‘C’. Agar hum ye tino length ko nikal lete hain to hamara kam asan ho jayega. Toh Chaliye ek ek karke apko batata hu in sab ko hum kaise nikalenge.

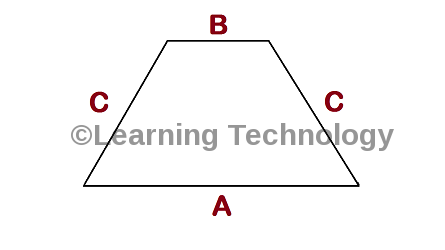
To sab se pehle mai apko batata hu ‘A’ ka lenth kaise nikalna hain.

‘A’ ka length nikalna bahut asan hain. Agar ap niche diye hue formula ko dekhenge to samajh jayenge.

Contents

1 CUTTING LENGTH OF TRAPEZIUM SHAPE STIRRUPS

CALCULATION OF ‘A’

(Length of Column) – (2 x Clear Cover)

= 600 – (2 x 40)

=600 – 80

= 520 mm

Ab hum nikalenge ‘B’ ka length.

‘B’ ka length nikalne ke lie apko ‘Centre to Centre Distance of Main Vertical Bar’ ka help lena hoga. Is lie maine apko ye pehle hi nikal lene ke liye kaha tha.

CALCULATION OF ‘B’

(C/C distance of Main Vertical Bar) + (2 x Half of Main Vertical Bar Dia) + (2 x Stirrups Dia)

= 161 + (2 x 10) + (2 x 8)

= 161 + 20 + 16

= 197 mm

Ab main ‘C’ ka length kaise nikalnege ye batane ja raha hu. Ise bahut dhayan se samajhiyega.

‘C’ Nikalne ke lie main niche ek Figure diya hu. Use dhyan se dekhiye. Hame yaha pe Pythagoras Theorem ko apply karna hoga. Pythagoras Theorem apply karne ke lie hame chahiye 3 variable, jaise ki Perpendicular yani ki HEIGHT, BASE aur HYPOTENUSE.

Jo ‘C’ hum nikalne wale hain wo hi hain hamara HYPOTENUSE. Ab hame niche diye hue Figure se samajhna hoga ki HEIGHT aur BASE ke length hum kaise nikalenge. To Chaliye main ye batata hu apko. Dhayan dijiyega.

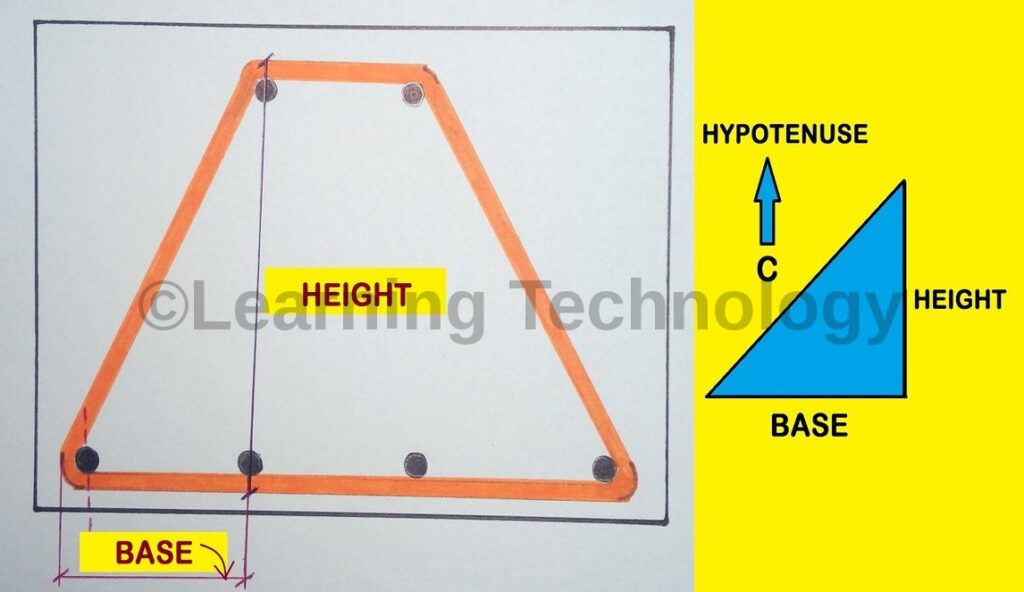
HEIGHT nikalna aasan hain. Apko Bas Breadth of Column se Clear Cover ko minus kar dena hga.

HEIGHT = Breadth of Column – (2 x Clear Cover) = 400 – (2 x 40) = 400 – 80 = 320 mm

Ab hum nikalenge BASE ka length.

Agar ap Figure ko gaur se dekhenge to ap samajh payenge ki BASE nikalne ke lie bhi hame ‘Centre to Centre Distance of Main Vertical Bar’ ka help lena padega.

Agar hum Right Side ko fix rakh kar left ki taraf badhte jaye, yani ki Stirrups ki Outer Face tak, to hume BASE ka length mil jayega. Niche diye hue formula ko dekhiye,

BASE = C/C Distance of Main Vertical Bar + (Half of Main Vertical Bar Dia) + (Dia of Stirrups)

= 161 + 10 + 8

= 179 mm

Hame ‘C’, yani ki HYPOTENUSE nikalne ke lie, HEIGHT aur BASE malun chal gaya hain. Ab Hum ‘C’ nikal sakte hain. To chaliye ‘C’ ka length nikal lete hain.

CALCULATION OF ‘C’

= Square root of { (BASE)^2 + (HEIGHT)^2}

= Square root of { (179)^2 + (320)^2}

= Square root of (32041 + 102400)

= 367 mm

Bas Apna kam ab asan ho gaya hain. Ab hum bas ek simple se formula ko use kar ke Cutting Length of Trapezium Shape Stirrups ko nikal sakte hain.

CUTTING LENGTH OF TRAPEZIUM SHAPE STIRRUPS

= A + B + (2 X C) + HOOK – BEND

Upar diye hue formula me ‘A’ , ‘B’, aur ‘C’ hame pata hain.

HOOK maine yaha consider kiya hain (10d), where ‘d’ is the diameter of the Stirrups. HOOK ka value apko apne Structural Consultants ke diye hue drawing se mil jayega. Aur agar nahi diya hai to ap 10d consider kar sakte hain. To hamara HOOK ka value nikalne ke lie niche dekhe :

HOOK = (2 x 10d) = (2 x 10 x 8) = 160 mm

Ab baat ati hain Bend Deduction ki. To figure me hum dekh sakte hain ki yaha pe 4 bend aisa hai jiska angle 135 degree hai aur 1 bend aisa hai jiska angle approx 45 degree hai. To hum 1 – 135 degree ke lie ‘3d’ deduct karenge aur 1 – 45 degree ke lie ‘1d’ deduct karenge. To hamara BEND deduction ka value ho jayega :

BEND DEDUCTION for 135 degree = (4 x 3d) = (4 x 3 x 8) = 96 mm

BEND DEDUCTION for 45 degree = (1 x 1d) = (1 x 1 x 8) = 8 mm

Ab ap dhayan se dekhiye jo value main formula me put kar raha hu.

= A + B + (2 X C) + HOOK – BEDN

= 520 + 197 + (2 x 367) + 160 – 96 – 8

= 1507 mm, OR 1.507 metre

Below I Have Uploaded My Hand Made Documents For You Only On Your Request, So That You Can Download It From Here. But One Thing Keep In Mind That This Is Only The Hand Made Notes.

If You Want Detailed Knowledge Then Watch My Video On YouTube Channel : Civil Learning Technology. I Am Telling This Because Many Important Points I Cover During Making Of Video, So If You Want To Know In Detail Then Watch My Video On YouTube Which is Given Below.